Group Diffusion Policy Optimization - Improving Reasoning for Diffusion Language Models

Kevin Rojas1,*, Jiahe Lin2, Kashif Rasul2, Anderson Schneider2, Yuriy Nevmyvaka2, Molei Tao1,✝, Wei Deng2,✝
1Georgia Institute of Technology 2Morgan Stanley
* Work done while interning at Morgan Stanley ✝ Correspondence
Paper Code

GDPO improves reasoning for diffusion language models by leveraging efficient variance-reduced sequence-level likelihood approximations instead of token level likelihood approximations

Introduction

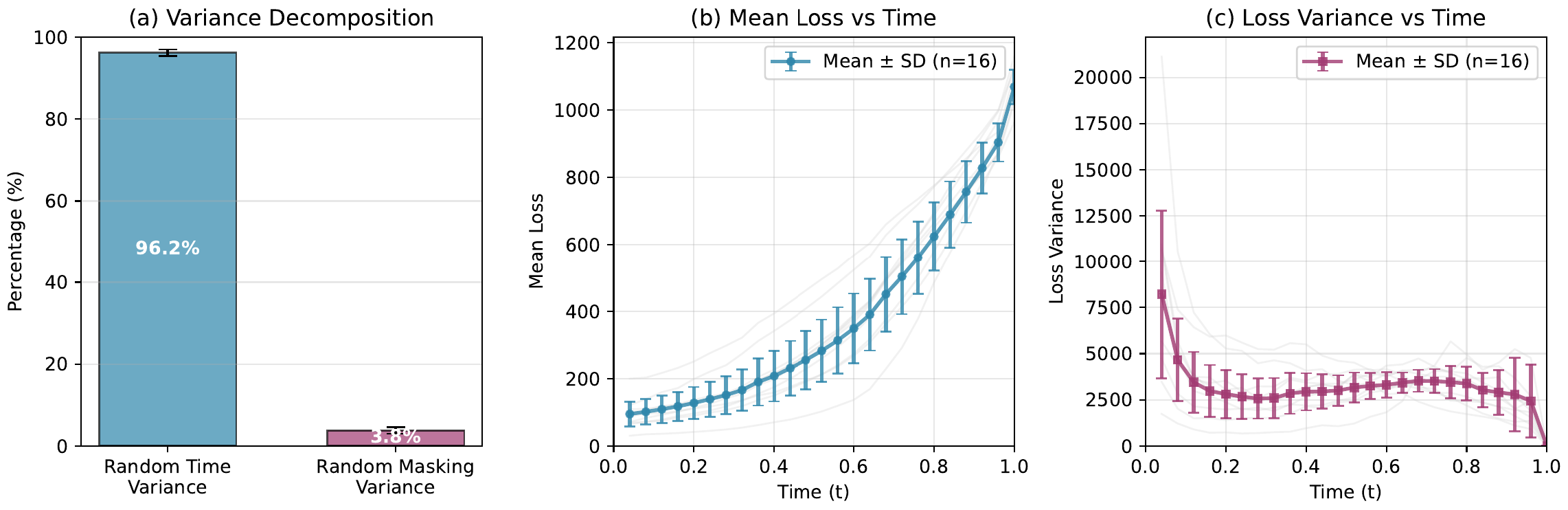
There has been an ongoing effort to adapt reinforcement learning (RL) algorithms for LLMs to DLMs. Most works have considered extending GRPO by finding ways to approximate the token-level likelihoods. However, this approach often comes with significant biases or computational inefficiencies. A more principled foundation lies in sequence-level likelihoods, where the ELBO serves as a surrogate. Yet, despite this clean mathematical connection, ELBO-based methods have seen limited adoption due to the prohibitive cost of likelihood evaluation.

In this work, we present efficient ways to estimate the ELBO for DLMs and leverage it to improve reasoning for DLMs. We introduce Group Diffusion Policy Optimization (GDPO), a new RL algorithm tailored for DLMs that leverages these efficient ELBO approximations to improve reasoning for DLMs. Our work leads to new SOTA results in finetuning LLada!

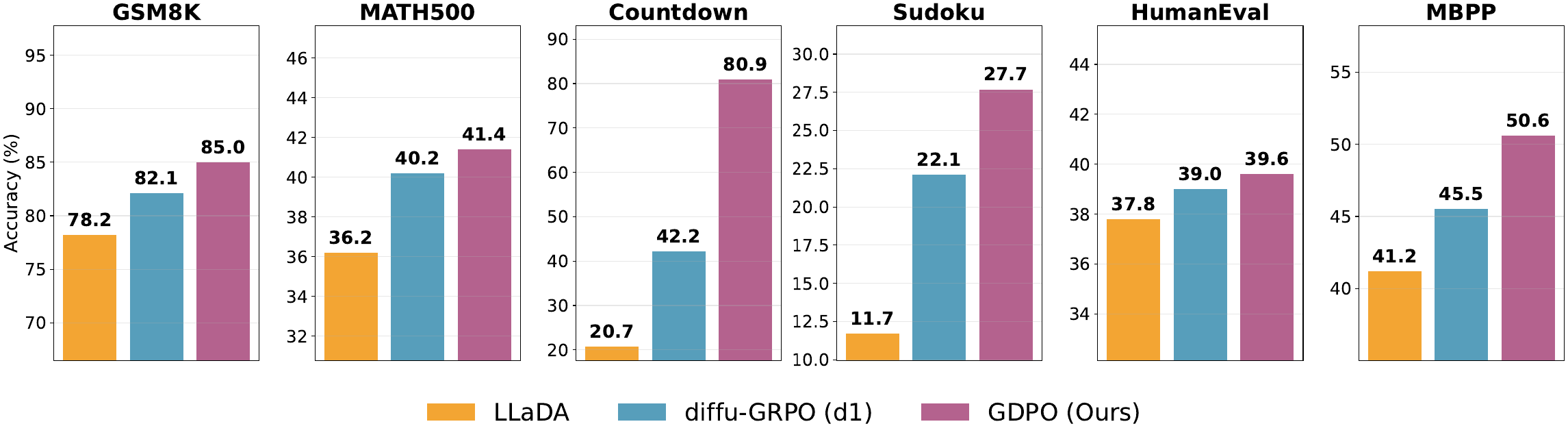
GDPO achieves new SOTA results in finetuning LLada on a variety of reasoning tasks.

Efficient ELBO Approximations

The ELBO for DLMs can be written as; $$ \mathbb{E}_{t\sim \mathcal{U}[0,1]} \mathbb{E}_{y_t \sim \pi_t(\cdot|y)} \left[ \frac{1}{t} \sum_{i = 1}^L \mathbf{1}[y_t^i = M] \log \pi_\theta(y^i|y_t, q)\right] \leq \log \pi(y|q), $$ This is usually approximated by a double monte carlo estimate. However, doing so leads to high variance, requiring many samples to get a good estimate. Our investigation reveals that most of the variance in approximating the ELBO comes from sampling in the time dimension.

Most of the variance in approximating the ELBO comes from the time dimension. The loss function also has a simple form making numerical Quadratures efficientto approximate the ELBO.

For this reason, we propose to approximate the ELBO as a time integral of a function instead of a double monte carlo estimate. This leads to efficient well grounded approximations by leveraging Gaussian Quadratures. $$ \int_0^1 \mathbb{E}_{y_t \sim \pi_t(\cdot|y)} \left[ \frac{1}{t} \sum_{i = 1}^L \mathbf{1}[y_t^i = M] \log \pi_\theta(y^i|y_t, q)\right] dt \leq \log \pi(y|q), $$ Notably, this leads to a provably lower-variance estimator!

Group Diffusion Policy Optimization (GDPO)

To leverage our new efficient ELBO approximation we propose Group Diffusion Policy Optimization (GDPO) which modifies the GRPO objective to use ELBO surrogates instead of token-level likelihoods. Formally, the GDPO loss is defined as: $$ \mathcal{L}^{\text{GDPO}}(\theta) = \mathbb{E}_{x}\mathbb{E}_{y_g \sim \pi_\theta^{\text{old}}} \left[ \frac{1}{G} \sum_{g=1}^G \frac{1}{|y_g|}\min\left( r_{g} A_g, \text{clip}(r_{g}, 1 - \epsilon, 1 + \epsilon) A_g \right) - \beta KL(\pi_\theta || \pi_{\text{ref}})\right] , $$ where the importance weights and advantage estimates are both done at the sequence level: $$ r_{g}(x) = \frac{\mathcal{L}_{\text{ELBO}}(y_{g} |x)}{\mathcal{L}_{\text{ELBO}}^{\text{old}}(y_{g}|x)}, \quad % A_g = \frac{R_g - \text{mean}(R_1, \dots, R_G)}{\text{std}(R_1, \dots, R_G)}. A_g = R_g - \text{mean}(R_1, \dots, R_G). $$ Here $\mathcal{L}_{\text{ELBO}}^{\text{old}}$ represents the ELBO evaluated under the old policy and $R_g = R(q,y_g)$, and we utilize unnormalized advantage estimates to avoid the bias of normalized advantage estimates.

BibTeX

@article{rojas2025improving,
  title={Improving Reasoning for Diffusion Language Models via Group Diffusion Policy Optimization},
  author={Rojas, Kevin and Lin, Jiahe and Rasul, Kashif and Schneider, Anderson and Nevmyvaka, Yuriy and Tao, Molei and Deng, Wei},
  journal={arXiv preprint arXiv:2510.08554},
  year={2025}
}